Преимущества и недостатки уравнения NRTL [3].

При помощи трехпараметрического уравнения NRTL можно, как правило, достаточно хорошо представит данные о равновесии в бинарных системах. Преимущество этого уравнения по сравнению с уравнениями Маргулеса и Ван-Лаара состоит в том. Что его можно применять к многокомпонентным смесям, основываясь только на бинарных параметрах, а по сравнению с уравнениями Вильсона – в том, что его можно использовать для представления равновесия жидкость-жидкость, хотя уравнение Цубоки-Катаямы-Вильсона также применимо в этих целях. В некоторых случаях какое-либо одно из уравнений дает лучшие результаты при описании равновесия пар-жидкость, но поскольку уравнение NRTL трехпараметрическое, оно обычно предпочтительнее, чем уравнение Вильсона или UNIQUAC.

При выводе уравнения UNIQUAC ,носившим получеткий характер, Абрамс и Праузниц исходили из модели двух жидкостей и концепции локального состава. Используемая ими модель предполагает, что избыточная энергия Гиббса обусловлена, во-первых, различием размеров и форм молекул (конфигурационная или комбинаторная составляющие) и, во-вторых, энергией взаимодействия молекул (вторая составляющая избыточной энергии Гиббса) [3].

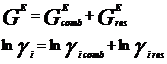
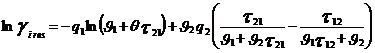
gi – параметр площади компонента i; ri – параметр объема компонента i;z – координационное число;- комбинаторная часть коэффициента активности компонента i; - остаточная часть активности компонента i;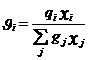- доля площади компонента i; 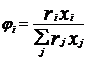- объемная доля компонента i.

По качеству описания равновесий жидкость – пар и жидкость – жидкость модель UNIQUAC в среднем соответствует модели NRTL, но содержит, в расчете на пару компонентов, на один оцениваемый параметр меньше. Последнее важно при расчете параметров для бинарных систем с малой взаимной растворимостью компонентов, когда для обоснованного расчета трех параметров данных недостаточно, а также в любом другом случае очень ограниченной экспериментальной информации о системе. Ценное свойство модели – учет в явной форме комбинаторного вклада в GЕ, что позволяет применить модель к растворам полимеров [7].

Сравнение уравнений.

Уравнение Маргулиса, Ван Лара и связанные с ними алгебраические выражения характеризуются относительной простотой математического аппарата, легкостью оценки параметров по данным о коэффициентах активности и адекватным представлением двухкомпонентных смесей, значительно отклоняющихся от идеальных, включая частично растворимые жидкие системы. Эти уравнения не применимы к многокомпонентным системам, если отсутствуют параметры взаимодействия между тремя и более компонентами.

Уравнение Вильсона позволяет точно представить равновесие пар – жидкость в двух- и многокомпонентных смесях с использованием только параметров бинарного взаимодействия. В силу большей простоты этого уравнения его использование может быть предпочтительным для решения указанной задачи, чем применение уравнений NRTL и UNIQUAC. Уравнение Вильсона нельзя непосредственно применять для представления равновесия жидкость – жидкость; использование в этих целях его столь же простой модификации, уравнения Цубуки – Катаямы – Вильсона, дает удовлетворительные результаты, хотя последнее не было подвергнуто тщательной экспериментальной проверке, как другие уравнения.