Для умеренно неидеальных бинарных смесей хорошие результаты дают все уравнения, содержащие два (или более) параметра бинарного взаимодействия; в таких случаях нет смысла разбирать преимущества той или иной модели. Следует только отметить, что старые модели (Маргулеса, Ван-Лаара) математически проще, чем более современные (Вильсона, NRTL, UNIQUAC).

Уравнение Маргулеса является наиболее старым из числа применяемых в настоящее время. Исследования Маргулеса были выполнены еще до того, как были сформулированы такие понятия, как фугитивность и коэффициенты активности, однако в сущности его предложения сводятся к представлению lnγ1 и lnγ2 в виде степенных рядов по составу:

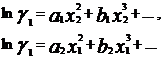для двухкомпонентных смесей.

Как правило, применяют линейные перегруппировки этих рядов, предложенные Карлсоном и Кольборном [3]:

в которых существует постоянная зависимость между параметрами и коэффициентами активности при бесконечном разбавлении:

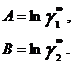
Избыточная энергия Гиббса, соответствующая этим уравнениям, составляет

Двухчленное (однопараметрическое) уравнение Маргулеса применимо только для простых смесей, в которых компоненты похожи по химической природе и размеру молекул [4].

Ван-Лаар рассмотрел изобарный процесс образования жидкого раствора из компонентов, включающий стадии испарения чистых веществ, их смешения в разреженном идеальном газовом состоянии и последующего сжатия и конденсации смеси до исходного давления. Он допускал нулевые значения избыточных объемов и энтропии процесса (соответственно, избыточная энергия Гиббса равна избыточной внутренней энергии) и подчинение флюидных фаз уравнению состояния Ван-дер-Ваальса, причем константы этого уравнения для смесей он представил с помощью простых комбинационных правил на основе констант для чистых компонентов [7]. Ван-Лаар просуммировал изменение внутренней энергии на отдельных стадиях процесса образования раствора, результат может быть представлен в виде следующих уравнений для GE и γi в бинарной системе:

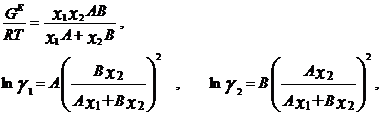
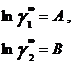
В модели Ван-Лаара величины А, В аналитически связаны с константами уравнения Ван-дер-Ваальса, однако выяснилось, что последние не обеспечивают адекватное описание систем, в частности, из-за большой чувствительности модели к произвольно выбранным комбинационным правилам для констант уравнения состояния. Если же рассматривать величины А, В как самостоятельные эмпирические параметры, оцениваемы по экспериментальным данным о бинарной системе, тогда соотношения превращаются в простые корреляционные уравнения, удовлетворительно описывающие многие системы[7].

Точность представленных выше моделей обычно удовлетворительна для систем малой или умеренной неидеальности и недостаточна для систем с большими отклонениями от идеального поведения.