Рассмотрим две различные физически возможные ситуации, связанные с вращением вокруг некоей фиксированной точки – центра. В данном разделе мы, не стремясь к излишней строгости изложения, ограничимся физическими аналогиями и подходом к анализу криволинейного движения, заимствованным из классической теоретической механики.

1. В первом случае представим себе вращательное движение двухатомной молекулы вокруг её центра масс. Пренебрегая относительно небольшими колебательными деформациями химической связи, можно считать постоянным межъядерное расстояние R, а соответственно, и радиусы сфер, по которым перемещается каждый из атомов вращающейся молекулы с массами и . Такая модель называется жёстким ротатором и может рассматриваться как пример чистого вращения (рис. 1)

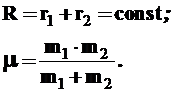
Рис. 1. Жесткий ротатор.

Ему отвечает кинетическая энергия

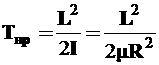(1)

где L– момент импульса, I – момент инерции, а – приведенная масса,

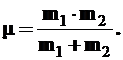
В свободном вращательном движении потенциальная энергия отсутствует, и оператор кинетической энергии представляет собой одновременно оператор полной энергии. Он запишется так:

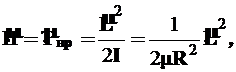где R=const (2)

Напомним читателю, что выражение оператора момента импульса I дано в разделе 2.2. Следует ожидать, что в сферических координатах оператор вр должен зависеть только от угловых переменных, но не от радиуса . Это легко проверить с помощью анализа размерности.

2. Второй случай сложнее и полнее. Он имеет место при движении одного электрона в поле ядра атома водорода, водородоподобном ионе или при взаимном вращении частиц в электрон-позитронной системе, известной как атом позитрония. Такое движение называется центральным, а сама задача Кеплеровой.

Электрон невозможно зафиксировать на сфере постоянного радиуса – это запрещено принципом неопределенности. При движении электрона как бы образуется пространственное облако. Тем не менее, можно обратиться к аналогии с классической механикой, которая позволяет в любом криволинейном движении выделить нормальную (радиальную) и тангенциальную (касательную) компоненты. Тангенциальная составляющая кинетической энергии соответствует чистому вращению – перемещению по сфере – и связана с моментом импульса формулой (1).

Движение электрона, порождающее облако с вероятностным распределением плотности, можно условно представить как совокупность чистых вращений на концентрических сферах с фиксированными радиусами и радиальных перемещений между этими сферами. В таком случае чисто вращательное слагаемое в составе оператора кинетической энергии также описывается формулой (2) но при этом момент инерции является переменной величиной из-за меняющегося радиуса

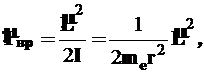(3)

где – масса электрона, а .

Присутствие радиального слагаемого в этом случае заставляет представить оператор кинетической энергии в виде суммы

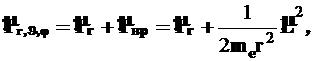(4)

3. В силу того, что оператор кинетической энергии частицы отличается от лапласиана только множителем (см. уравнение 2.15), домножив на него формулу (4.46), получим

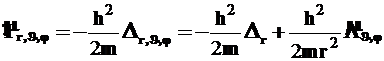(5)

Сравнивая формулы (4.50) и (4.51), приходим к фундаментальному соотношению

, (6)

т.е. оператор квадрата момента импульса совпадает с оператором Лежандра с точностью до постоянного множителя . Заметим, что размерность собственных значений оператора совпадает с размерностью постоянной Планка .