Модели задачи пространственного вращенияПериодическая система / Модели задачи пространственного вращенияСтраница 2
4. Этот же результат можно получить и последовательными математическими преобразованиями компонент операторов ![]() и
и ![]() . Процедура перехода к сферическим координатам для компонент
. Процедура перехода к сферическим координатам для компонент ![]() аналогична той, что была осуществлена в разделе. при переводе
аналогична той, что была осуществлена в разделе. при переводе ![]() к плоской полярной системе координат. Кстати говоря, в сферических координатах
к плоской полярной системе координат. Кстати говоря, в сферических координатах ![]() имеет тот же самый вид. Используя уравнения и читатель сам легко получит выражения
имеет тот же самый вид. Используя уравнения и читатель сам легко получит выражения
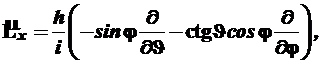 (7)
(7)
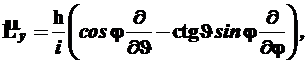 (8)
(8)
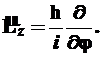 (9)
(9)
Суммируя результаты возведения в квадрат найденных выражений для операторов проекций момента импульса, получаем формулу (6), которая в развернутой форме с учетом имеет вид
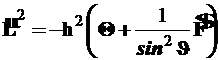 (10)
(10)
5. Жесткий ротатор. Уравнение Шредингера.
5.1. Согласно вышеизложенному, уравнение Шредингера для жесткого ротатора может быть представлено так
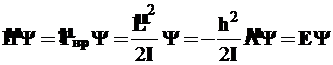 (11)
(11)
Поскольку момент инерции постоянен (I=const), волновые функция жёсткого ротатора с точностью до постоянного множителя совпадают с собственными функциями оператора Лежандра. Последние обозначаются символом ![]() и носят название шаровых, или сферических функций. Это значит, что должно быть справедливым операторное уравнение, следующее из (11)
и носят название шаровых, или сферических функций. Это значит, что должно быть справедливым операторное уравнение, следующее из (11)
![]() (12)
(12)
где ![]() – собственное значение оператора Лежандра, связанное с квадратом момента импульса и энергией вращения;
– собственное значение оператора Лежандра, связанное с квадратом момента импульса и энергией вращения;
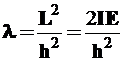 (13)
(13)
5.2. Поэтому следующий этап решения нашей задачи состоит в нахождении собственных функций операторного уравнения (4.57), которое в развёрнутом виде представляется так
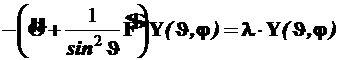 (14)
(14)
Конструкция уравнения (14), включающего сумму операторов, каждый из которых содержит одну переменную, позволяет легко произвести разделение переменных, используя метод Фурье.
5.3. Для этого представим функцию ![]() в виде произведения
в виде произведения
![]() , (15)
, (15)
умножим обе части уравнения (14) слева на ![]() и перегруппируем слагаемые, включающие разные переменные:
и перегруппируем слагаемые, включающие разные переменные:
 (16)
(16)
Переменные ![]() и
и ![]() полностью разделились, поэтому правую и левую его части можно приравнять одной и той же постоянной. В результате получится два независимых уравнения
полностью разделились, поэтому правую и левую его части можно приравнять одной и той же постоянной. В результате получится два независимых уравнения
![]() (17)
(17)
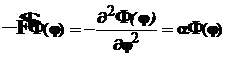 (18)
(18)
5.4. Уравнение (17) – это уравнение Шредингера для плоского ротатора, где ![]() , и решение его было предметом обсуждения в разделе 3.2:
, и решение его было предметом обсуждения в разделе 3.2:
![]() , где
, где ![]() (19)
(19)
причём квантовое число m связано с квантованием проекции момента импульса на ось z, так как изменение угла ![]() описывает вращение вокруг этой оси:
описывает вращение вокруг этой оси:
![]()
6. Множитель![]() пока ещё не раскрыт, однако ясно, что каждая волновая функция
пока ещё не раскрыт, однако ясно, что каждая волновая функция ![]() отвечает состоянию с некоторым определенным фиксированным квадратом момента импульса или, что то же самое, с фиксированным модулем момента импульса. Обратим внимание читателя на то, что все преобразования, начавшись как векторные, завершаются расчетами в скалярной форме, и понятно, что из таких расчётов естественном путём вытекает квантование абсолютного значения векторной величины в виде квантования ее квадрата. Необходимое квантовое число назовем l и далее получим его значение.
отвечает состоянию с некоторым определенным фиксированным квадратом момента импульса или, что то же самое, с фиксированным модулем момента импульса. Обратим внимание читателя на то, что все преобразования, начавшись как векторные, завершаются расчетами в скалярной форме, и понятно, что из таких расчётов естественном путём вытекает квантование абсолютного значения векторной величины в виде квантования ее квадрата. Необходимое квантовое число назовем l и далее получим его значение.
Смотрите также
Способы получения алюминия
Алюминий является
важнейшим металлом, объем его производства намного опережает выпуск всех
остальных цветных металлов и уступает только производству стали. Высокие темпы
прироста производст ...
Таллий (Thallium), Tl
Знаменитый Крукс, был большим специалистом по спектроскопии. Прекрасно понимая, что спектроскоп - мощный инструмент отыскания новых элементов, Крукс исследовал с его помощью огромное количество различ ...
Скорость химической реакции
Вокруг нас постоянно происходят тысячи химических реакций. Горит
костер и горит газ в конфорке газовой плиты, ржавеет железо, молоко
превращается в творог, на фотопленке возникают изображени ...
