, .(6.7)

Тогда решениями приведенного уравнения (6.5) будут

;(6.8)

;(6.9)

,(6.10)

от которых заменой

(6.11)

снова можно перейти к решениям кубического уравнения (6.4).

3. Вычислим характеристические константы уравнения Ван-дер-Ваальса. Для удобства вычислений примем следующие единицы измерения: V - л/моль , P - атм, Т - К. Тогда R = 0,08206 л·атм/(моль·К);

a = 27·0,082062·6502/(64·31)=38,72 л·атм;

b = 0,08206·650/(8·31)=0,2151 л.

4. Давление насыщения находится методом последовательных приближений. В качестве первого приближения при Т = 400 К примем давление насыщения равным 10 атм.

5. Рассчитаем значения коэффициентов уравнения (6.4):

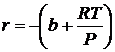= –(0,2151+0,08206·400/10) = – 3,4975;

= 38,72/10 = 3,872;

= – (38,72·0,2151/10) = – 0,8329.

6. Далее вычислим коэффициенты приведенного кубического уравнения (6.5) и значение дискриминанта D:

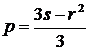= [3·3,872–(–3,4975)2]/3 = – 0,2055;

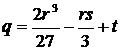= 2·(–3,4975)3/27–(–3,4975·3,872)/3+(–0,8329)=0,5121;

= (–0,2055/3)3+(0,5121/2)2 = 0,0652.

Значение дискриминанта (D) получилось положительным, что говорит о единственном действительном решении уравнения (6.5). Следовательно, значение давления выбрано неверно.

7. Предположим, что давление насыщения равно 1 атм. Повторим вычисления в пунктах 5 и 6.

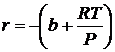= –(0,2151+0,08206·400/1) = –33,04;

= 38,72/1 = 38,72;

= –(38,72·0,2151/1) = –8,329;

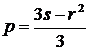=[3·38,72 –(–33,04)2]/3 = –325,2;

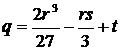= 2·(–33,04)3/27 –(–33,04·38,72)/3+(–8,329) = –2254;

= (–325,2/3)3+(–2254/2)2 = –3632.

Значение D отрицательное, следовательно, уравнение имеет три действительных решения.

8. Найдем эти решения, но прежде вычислим вспомогательные величины и .

= [–(–325,2)3/27]1/2 = 1129;

= –(–2254)/(2·1129) = 0,9982;

= arccos (0,9982) = 0,0600 радиан;

= 2·(1129)1/3·cos(0,0600/3) = 20,82;

= 2·(1129)1/3 cos(0,0600/3 + 2·3,14/3) = –10,75;

= 2·(1129)1/3 cos (0,0600/3 + 4·3,14/3) = –10,09.

9. Перейдем к решениям уравнения (6.4), воспользовавшись (6.11).