Нахождение условий насыщения из уравнений состояния представляет собой достаточно сложную задачу, решение которой зачастую невозможно без привлечения вычислительной техники и специального программного обеспечения. Для простых уравнений состояния, таких как уравнение Ван-дер-Ваальса, эта задача может быть решена путем несложных вычислений. Однако необходимо помнить, что на практике при помощи уравнения Ван-дер-Ваальса можно лишь качественно оценить состояние насыщения. Для более точного представления насыщения разработаны другие уравнения состояния и специальные методы.

В данном пособии на примере уравнения Ван-дер-Ваальса рассмотрен подход к нахождению давления насыщения и объемов насыщения жидкости и пара (точки, принадлежащие бинодали), а также условий, определяющих метастабильные состояния вещества (точки экстремумов изотермы).

Пример 6.3

Для изобутилбензола при температурах 400, 500, 600 и 640 К, используя уравнение Ван-дер-Ваальса, рассчитать давление пара и объемы насыщения жидкости и пара. Определить также области метастабильных состояний пара и жидкости при указанных температурах. Критическая температура равна 650 К, критическое давление - 31 атм.

Решение

1. Запишем принцип Максвелла:

Площадь = .(6.1)

Выразим из уравнения Ван-дер-Ваальса значение давления и подставим его в подинтегральное выражение. Получим

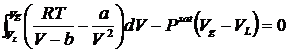.(6.2)

В данном случае имеется возможность найти аналитическое решение определенного интеграла

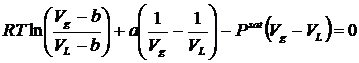.(6.3)

Теперь задача сводится к отысканию значения P sat, при котором выражение 6.3 обратится в тождество. При его нахождении нам потребуется неоднократно определять значения объемов жидкости и пара для заданного P, т.е. находить решения (корни) кубического уравнения.

2. Перепишем уравнение Ван-дер-Ваальса в виде полинома по объему

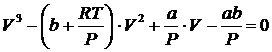.(6.4)

Корни данного уравнения можно найти, воспользовавшись формулами Кардано. Для этого перейдем к приведенному виду кубического уравнения, выполнив следующие преобразования. Обозначим коэффициенты в уравнении (6.4) через

; ;

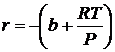и сделаем замену неизвестного V на Y:

;

тогда уравнение (6.4) примет приведенный вид

,(6.5)

где ; .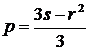

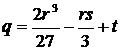Число действительных решений кубического уравнения зависит от знака дискриминанта

.(6.6)

Если D > 0, то уравнение имеет одно действительное решение; если D < 0, то - три действительных решения; и если D = 0, то уравнение имеет либо два действительных решения, одно из которых двукратное, либо одно действительное трехкратное решение (последнее в случае p = q = 0).

В данном примере рассматривается область P-V-T пространства, где сосуществуют пар и жидкость. Для этой области уравнение Ван-дер-Ваальса имеет три действительных решения (дискриминант уравнения (6.5) меньше нуля). При использовании формул Кардано в оригинальном виде корни уравнения выражаются через комплексные величины. Избежать этого можно, если ввести следующие обозначения: