Разложение представления в прямую сумму неприводимых представлений
с помощью оператора ВигнераМатериалы / Теория симметрии молекул / Разложение представления в прямую сумму неприводимых представлений
с помощью оператора ВигнераСтраница 2
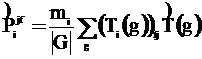. (40)
Из соотношений ортогональности для матриц неприводимых представлений следует, что этот оператор дает возможность получить eigs по формуле
, i=1, 2, …, t. (41)
Все сказанное можно выразить в виде следующего алгоритма.
Для того, чтобы найти базу модуля М из элементов, преобразующихся по неприводимым представлениям Тi, содержащихся в представлении Т, связанном с модулем М, необходимо:
1.По формуле (32) найти размерности подпространств Мij, соответствующих j-компоненте неприводимого представления Ti.
2.Найти с помощью оператора проектирования (39) все подпространства Mij.
3.В каждом подпространстве Mij выбрать произвольную ортонормированную базу.
4.Используя формулу (41), найти все элементы базы, преобразующихся по остальным компонентам неприводимого представления Тi.
Смотрите также
Исследования Николая Зинина
Николай
Зинин родился 13 (25) августа 1812, г. Шуша Елизаветпольской губернии,
ныне в Нагорном Карабахе. Скончался 6 (18) февраля 1880, в Петербурге.
...
Принципы динамической организации
...
Основные пути развития торговли
Торговля — это особая деятельность людей, связанная с осуществлением актов купли — продажи и представляющая собой совокупность специфических технологических и хозяйственных операций, напра ...