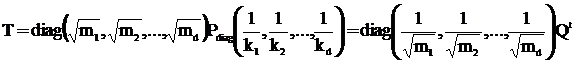
где k1, k2, …, kd – мощности классов сопряженных элементов, mi определяются по формуле mi=fi2, где fi – степени неприводимых представлений.

Теорема 2. Каждый столбец таблицы характеров является общим левым собственным вектором матрицы Ci, Cj, …, Cd, а каждая строка является общим правым собственным вектором этих матриц. И наоборот, каждый стандартный общий левый собственный вектор матриц Ci и, каждый стандартный общий правый собственный вектор этих матриц с точностью до расположения строк и столбцов является строкой и соответственно столбцом матрицы характеров.

Замечание. Собственный вектор матрицы называется стандартным, если его правая координата равна единице.