Определение 1. След матрицы А=(аij) размера n´n есть сумма ее элементов, стоящих по главной диагонали:

TrA=a11+a22+…+ann (14)

Определение 2. След матрицы Т(g), представляющий элемент g в матричном представлении Т группы G, называется характеристикой элемента g в представлении Т и обозначается cT(g).

Определение 3. Совокупность характеристик всех элементов g группы G, составленных для данного представления Т, называется характером представления Т и записывается как cT. Если Т – матричное представление группы G над полем вещественных или комплексных чисел Р, то характеристика каждого элемента группы является вещественным или комплексным числом и, следовательно, характер есть отображение cT группы G в поле Р, определяемое следующим образом:

cT: G®P: cT(g)=TrT(g).

Свойство 1. Характеры эквивалентных представлений совпадают.

Свойство 2. Характер представления Т группы G постоянен на каждом классе сопряженных элементов: cT(g-1hg)= cT(h), g, hÎG.

Определение 4. Вектор x¹0 из векторного пространства V над числовым полем Р называется собственным вектором линейного оператора , действующего в этом пространстве, если он удовлетворяет соотношению x=lx, где l - число, которое называется собственным значением (характеристическим числом) линейного оператора.

Условие того, что вектор х – собственный вектор записывается в виде матричного уравнения

(А - lI)х = 0, (15)

где х – вектор-столбец с неизвестными координатами x1, x2, …, xn. Условием существования ненулевого решения системы (15) является равенство нулю его определителя:

|A - lI| = 0. (16)

Это уравнение степени n относительно l называется характеристическим или вековым уравнением матрицы А линейного оператора, а его корни называются собственными значениями матрицы А, они являются собственными значениями оператора .

Свойство 3. Если l1, l2, …, ln – собственные значения линейного оператора , то cT(g)=TrT(g)= l1+l2+ …+ln.

Так как здесь рассматриваем конечные группы, то имеет место следующее свойство.

Свойство 4. Если Т – представление группы G над полем Р, то для каждого элемента gÎG значение cT(g) равно сумме корней из единицы степени, равной порядку элемента g.

Свойство 5. Если Т – представление группы G, то для каждого gÎG справедливо равенство cT(g-1)= cT(g).

Свойство 6. Если и - характеры неприводимых представлений группы G, то

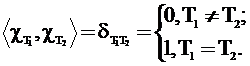(17)

Равенство (17) называется соотношением ортогональности, для характеров, неприводимых представлений группы G.

Свойство 7. (второе соотношение ортогональности) Пусть T1, T2, …, Tm – все неэквивалентные представления группы G, K(a), K(b) – классы элементов группы G, сопряженных соответственно с a и b. Тогда

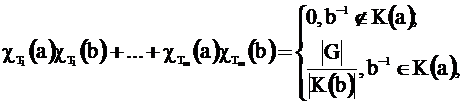(18)

где |G| - число элементов в группе G; |K(b)| - число элементов в классе сопряженных элементов K(b); - характеры неприводимых представлений Ti, i=1, 2, …, m.