Определение 5. Отображение множества М в множество N – это правило f, по которому каждому элементу m из множества M ставится в соответствие однозначно определенный элемент mf=n из множества N.

Определение 6. Гомоморфизмом группы G в группу G¢ называется отображение j множества G в множество G¢ такое, что

(1)

В качестве примера рассмотрим группу C3V и группу {-1}2, состоящую всего из двух элементов {-1}2={-1, 1}.

Построим отображение j группы C3V в группу {-1}2 (записываем это в виде j: C3V®{-1}2) по следующему правилу: элементам , , сопоставим 1, а элементам ,, сопоставим -1. Отображение j построено, причем, как видим, у элемента 1 группы {-1}2 есть три прообраза, т. е. три элемента группы C3V, образом каждого из которых является 1: у элемента –1 также три прообраза – это не запрещено определением отображения.

Покажем теперь, что j есть гомоморфизм. Из таблицы Кэли группы C3V видно, что произведение любых двух элементов множества C3={, , } принадлежит этому же множеству, в то же время . Из этой таблицы видно, что , i, j=1, 2, 3 принадлежит множеству C3, но с другой стороны, . Наконец, произведения и , i, j=1, 2, 3 принадлежат множеству , с другой стороны , . Таким образом для любых двух операций симметрии и из множества C3V получаем, что , где , , есть 1 или –1, т. е. отображение j, действительно есть гомоморфизм.

Определение 7. Отображение f множества М в множество N называется взаимно однозначным отображением множества М на множество N, если каждый элемент множества N является образом в точности одного элемента множества M.

Определение 8. Две группы G и G¢ называются изоморфными (обозначение G@G¢), если существует взаимно однозначное отображение q группы G на группу G¢ такое, что

(2)

Свойства группы или других математических объектов, сохраняющиеся при изоморфизме, называются структурными свойствами. Приведем два примера структурных свойств групп, которым предшествуют два важных определения.

Определение 9. Если группа G содержит конечное число элементов, то число n элементов группы называется порядком группы и обозначается n=|G|.

Например, |C3V|=6; |{-1}2|=2.

Определение 10. Группа называется абелевой или коммутативной, если для всех элементов a и b этой группы выполняется равенство ab=ba.

Так, группа {-1}2 является абелевой, а группа C3V не абелева.

Теорема 2. Если две конечные группы G и G¢ изоморфны, то их порядки равны.

Теорема 3. Если G – абелева группа и G@G¢, то и G¢ - абелева группа.

Теорема 4. Каждая конечная группа изоморфна некоторой группе перестановок и некоторой группе матриц.

Приведем пример. Пронумеруем элементы группы C3V в виде =1; =2; =3; =4; =5; =6. Используя таблицу Кэли группы C3V, запишем

.

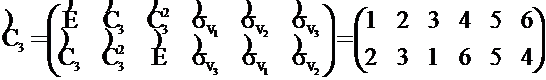Далее, получим, используя правило умножения перестановок. Ясно, что