Для малых и средних концентраций поверхностно-активных веществ (ПАВ) при описании зависимости = f(c) используется уравнение Шишковского:

,

Ответы подскажите состав хозяйственного мыла.

где s0 – поверхностное натяжение растворителя (Н/м);

c – концентрация поверхностно-активного вещества (ПАВ);

А, b – константы, данные в справочнике.

Уравнение Гиббса-Гельмгольца для поверхностной энергии. Полная поверхностная энергия

Запишем известное из термодинамики выражение внутренней энергии для поверхности.

Us = Gs + TSS - уравнение полной поверхностной энергии.

В этом уравнении qs = TDS - теплота образования единицы поверхности в обратимом процессе. Она равна количеству теплоты, которую необходимо подвести к системе, чтобы увеличить ее поверхность на единицу при T=const. Из уравнений фазы при постоянстве всех параметров, кроме температуры, имеем:

dGs = - SsdT,.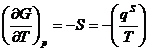

Подставляя эти значения в уравнение полной поверхностной энергии, получаем:

- уравнение Гиббса - Гельмгольца для поверхности.

Оно связывает полную поверхностную энергию с энергией Гиббса (поверхностное натяжение).

Для гетерогенной системы изменение внутренней энергии, исходя из I и II начал термодинамики:

dU =TdS – pdV +dS +idni +jdq,

где dU - изменение внутренней энергии;

dS - изменение энтропии;

dV - изменение объема;

Т – температура;

Р – давление;

- поверхностное натяжение;

n - число молей компонента;

dq - изменение электрического заряда;

- химический потенциал компонентов;

- электрический потенциал компонентов;

S - межфазная поверхность.

При S, V, n, q=const уравнение примет вид: dU =dS

,

т.е. - это изменение энтропии на единицу площади.

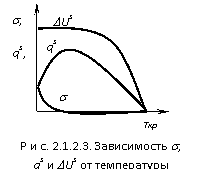
Из уравнений видно , т.е. подтверждается, что при увеличении температуры поверхностное натяжение снижается. Если сопоставить изменение , qs, Us от температуры, получим рис. 2.1.2.3. Из графика видно, что величина DUs для индивидуального вещества величина практически постоянная т.е. DUs не зависит от температуры. Для расчета зависимости = f(T) используются эмпирические и полуэмпирические зависимости - метод парохор, формула Этвеша.

В случае твердых фаз процесс образования новой поверхности носит необратимый характер и (поверхностное натяжение) можно изменить только косвенным путем, например, путем расчета. Мерой количественного выражения свободной энергии является f или G. В соответствии со вторым законом термодинамики для самопроизвольных процессов,

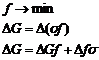
Возможны два варианта:

1.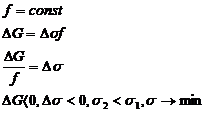2.

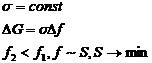
Отсюда следует, что в дисперсных системах в самопроизвольных процессах поверхность (а, следовательно, и поверхностное натяжение) уменьшается.