2.2.1. Возможные значения физически наблюдаемых величин являются собственными значениями операторных уравнений вида

Каждой динамической переменной ставится в соответствие свой линейный самосопряженный оператор.

2.2.2. Важнейшими динамическими характеристиками одной частицы являются:

- радиус-вектор , где координаты могут быть:

декартовыми или полярными ( - углы, а – длина вектора);

- вектор импульса и его координаты – проекции;

- вектор момента импульса , являющийся векторным произведением радиуса-вектора на импульс

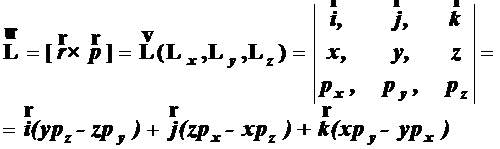(2.5)

и, соответственно, его проекции равны

(2.6)

(2.7)

(2.8

- кинетическая энергия Т,

скалярная величина, которая в поступательном движении связана и с массой и импульсом

;

для одномерного вращения вокруг оси (например, z

) справедлива подобная же формула, где масса заменена моментом инерции Iz

, а импульс – его моментом :

- потенциальная энергия, т.е. скалярное силовое поле, задаваемое функци-ей координат , в котором движется частица;

- полная энергия Е, равная сумме кинетической и потенциальной энергий

2.2.3. С учетом общих требований, предъявляемых к операторам квинтовой механики, постулируются простейшие операторы, а именно: операторы координат, определяющие положение частицы, и импульса ее,

- оператор координаты совпадает с умножением на саму координату q, т.е.: , или угол,

или, в общем виде ;

- оператор импульса имеет дифференциальную форму

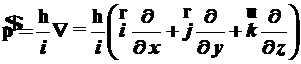(2.9)

где постоянная Планка Дж·с, и операторы координат импульса соответственно равны:

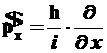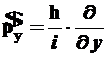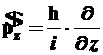, , (2.10)

Введение в оператор, мнимой единицы превращает его в самосопряженный т.е. отвечающий условию (1.5).

2.2.4. Остальные операторы строятся по формулам классической механики, где вместо координат и импульсов используются их операторы, Это утверждение можно считать следствием макроскопического устройства приборов по законам классической физики. Построим операторы и для одной частицы:

- операторы момента импульса и его проекций:

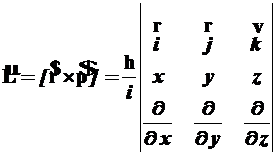, (2.11)

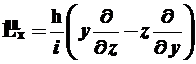, (2.12)

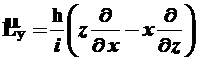, (2.13)

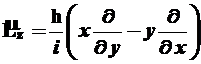(2.14)