(1.10)

Уравнение связи между векторным полем нод и скалярным полем равновесных температур [3, 6, 8] позволяет легко анализировать фазовое равновесие для многокомпонентных смесей. Данное уравнение записывается как система уравнений в частных производных и при имеет следующий вид:

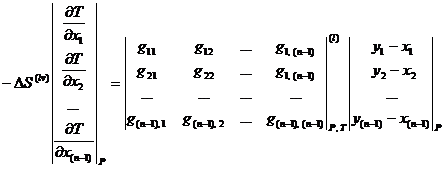(1.11)

Для случая :

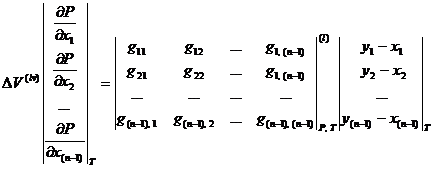, (1.12)

где – изменение энтропии при фазовом дифференциальном переходе бесконечно малого количества смеси из жидкости () в пар ();

– изменение объема при фазовом дифференциальном переходе бесконечно малого количества смеси из жидкости () в пар ();

– вторые производные изобарно-изотермического потенциала Гиббса для жидкой () фазы;

– концентрации -компонента в жидкой и паровой фазе соответственно.

В общем виде уравнения (1.11) и (1.12) можно представить так [3, 6, 8]:

, (1.13)

(1.14)

С помощью оператора в уравнениях (1.13) и (1.14) связывают вектор-ноду жидкость–пар и градиент температуры (при ) или градиент давления (при ). На рис. 1.4 приведена общая картина расположения векторов, взаимосвязанных уравнением фазового обмена [8].

Как видно, в первом случае векторы ноды и градиента температур направлены в разные стороны и образуют между собой тупой угол; во втором – векторы ноды и градиента давлений направлены в одну сторону и образуют между собой острый угол, что объясняет знак «–» в уравнении (1.11). После действия оператора G вектор ноды изменяет свое направление и модуль и становится вектором . Вектор градиента после умножения на скалярный множитель изменяет свой модуль и также становится равным по величине вектору .

(а) (б)

Рис. 1.4. Взаимное расположение изотермоизобарического многообразия, векторов ноды жидкость–пар и градиентов температуры (а) и давления (б) в трехкомпонентных системах.

Из сравнения уравнений (1.11) и (1.12) следует частный вывод. Для некоторого вектора состава жидкой фазы отнимем одно уравнение от другого. При определенных и получим следующий результат [8]:

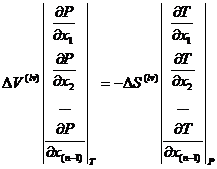(1.15)

или:

(1.16)

Поскольку и – некоторые скалярные множители, то для закрепленного состава системы градиенты стационарного поля температур кипения при и градиенты стационарного поля давлений при колинеарны. Последнее согласуется с физическим смыслом, так как в этом случае точка состава смеси принадлежит определенному изотермоизобарическому многообразию, которое является многообразием уровня как для температуры, так и для давления. Однако векторы имеют разный знак, и их линейная (в точке) комбинация всегда равна нулю: