(а) (б) (в)

Рис. 1.3. Особые точки траектории дистилляции в трехкомпонентных системах:

(а) – неустойчивый узел; (б) – устойчивый узел; (в) – седло.

Таковы закономерности векторного поля равновесных нод жидкость–пар. Далее рассмотрим закономерности скалярного поля равновесных температур.

Фазовое равновесие жидкость–пар многокомпонентных смесей можно рассматривать в диаграммах, отражающих зависимости скалярных свойств от вектора состава. Например, диаграмма равновесия может быть представлена полем равновесных температур кипения жидкой фазы системы при заданном давлении. На диаграммах состав–свойство для n-компонентной двухфазной системы любое свойство, выраженное некоторой скалярной величиной, не зависящей от времени, индуцирует над концентрационным симплексом непрерывное стационарное скалярное поле, структура которого усложняется с увеличением компонентности системы. Для трехкомпонентной системы диаграмма равновесия характеризуется некоторыми линиями, называемыми изотермоизобарами. Для четырехкомпонентных систем изотермоизобары являются уже некоторыми поверхностями и т.д. Скалярное стационарное поле равновесных температур может быть представлено и в векторном виде с помощью вектора-градиента. Этот вектор всегда направлен в сторону наибольшего возрастания поля (в данном случае поля температур) ортогонально к многообразию уровня. Вектор-градиент характеризуется набором частных производных величины свойства (температуры) по концентрациям компонентов:

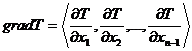(1.5)

Производная этого градиента по времени равна нулю, что отражает стационарность рассматриваемого поля:

(1.6)

Использование градиента позволяет представить скалярное поле в виде некоторых линий, в каждой точке которой направление касательной к этой линии задается градиентом, то есть мгновенная скорость продвижения по такой линии численно равна градиенту. Мгновенное изменение вектора состава, равное dX, будет также вектором, принадлежащим концентрационному симплексу и коллинеарному градиенту. Следовательно, имеем следующую функциональную зависимость:

(1.7)

Или теоретически можно представить себе движение фигуративной точки в поле градиента температуры, при котором в каждой точке траектории градиент лежит на касательной прямой к этой траектории. Такое движение описывается системой уравнений вида [6]:

(1.8)

Дифференциал температуры в общем виде представляется как скалярное произведение градиента температуры на вектор изменения состава одной из фаз. Для жидкой фазы:

(1.9)

Согласно уравнению (1.9), равенство нулю дифференциала равновесной температуры будет реализовываться в двух случаях:

1) Вектор-градиент равновесной температуры равен нулю , то есть равны нулю все частные производные скалярной величины по переменным концентрациям компонентов. Этот случай характеризует особую точку температурной поверхности размерности , которая может быть минимумом, максимумом, минимаксом.

2) Векторы и ортогональны друг другу, и их произведение равно нулю. Это условие соответствует движению вдоль изотермоизобарического многообразия, вдоль которого и .

Уравнение Ван-дер-Ваальса–Сторонкина [7] – это математическая модель, описывающая равновесное распределение всех компонентов между фазами и устанавливающая соответствие между параметрами фазового перехода. Также это уравнение фазового обмена, связывающее фазовые эффекты (объемный, энтропийный, эффект химических потенциалов), которые отражают локальное поведение системы при переходе бесконечно малого количества одной фазы в конечное количество другой фазы.

В общем виде для двухфазной -компонентной системы уравнение Ван-дер-Ваальса–Сторонкина записывается так [7]: