Под геометрической конфигурацией молекулы или иона будем понимать пространственное расположение ядер атомов в молекуле или ионе относительно друг друга. Геометрическую конфигурация молекулы можно охарактеризовать, построив модель молекулы. Впервые модели молекул из шаров и стержней были построены в 1810 г. Джоном Дальтоном. Современные представления о структуре молекулы являются более точными благодаря применению точных экспериментальных методов определения этой структуры (оптические и дифракционные методы). Использовав эти методы, мы можем построить геометрическую модель молекулы в виде конечной фигуры.

Важной особенностью современных представлений о строении молекул является наличие симметрии молекул.

Определение 1. Отображением множества M на множество N называется правило f, которое каждому элементу m из множества M ставит в соответствие элемент n из множества N, называемый образом элемента m, при этом каждый элемент множества N является образом хотя бы одного элемента из множества M.

Если M=N, то говорят об отображении множества М на себя.

Определение 2. Операцией симметрии конечной фигуры называется ее изомерическое (т. е. сохраняющее расстояние между точками фигуры) отображение на себя.

Рассматривая эти примеры, приходим к заключению, что помимо геометрической модели, с молекулой аммиака необходимо связать геометрические образы – прямую C3 и плоскость , которые не принадлежат модели хотя бы потому, что они бесконечны

Операции симметрии пространственной фигуры, соответствующей молекуле, называются операциями симметрии молекулы.

В качестве примера рассмотрим молекулу аммиака NH3. Ее геометрическая конфигурация имеет форму правильной треугольной

О1

Рис. 1 пирамиды.

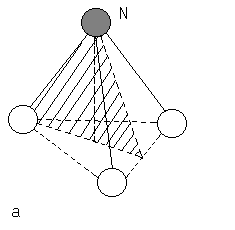
К числу операций симметрии правильной треугольной пирамиды относятся повороты, совмещающие ее с собой. Точки N и O определяют ось поворота, которую обозначим через С3. Повернем пирамиду вокруг этой оси на 120о против часовой стрелки. Указанный поворот обозначим через . На рис. 1, б изображена фигура (результат поворота), которая совмещается с исходной (рис. 1, а) при наложении. Рассмотрим отражение в плоскости , совмещающее фигуру с собой, и обозначим его . Очевидно, что , как и , является операцией симметрии молекулы аммиака, так как операции и не изменяют расстояний между точками фигуры NH3.

Рассматривая эти примеры, приходим к заключению, что помимо геометрической модели, с молекулой аммиака необходимо связать геометрические образы – прямую C3 и плоскость , которые не принадлежат модели хотя бы потому, что они бесконечны.

Определение 3. Элементом симметрии молекулы называется вспомогательный геометрический образ (точка, прямая, плоскость), характеризующий некоторое множество операций симметрии фигуры, изображающей молекулу.

Например, ось C3 характеризует множество операций симметрии, состоящее из рассмотренного нами поворота , а также поворотов на 240о и на 360о против часовой стрелки молекулы аммиака. Поворот называется тождественной операцией симметрии. При этой операции симметрии все точки геометрической модели молекулы отображаются в себя. Плоскость характеризует множество операций симметрии, состоящее из и .