Зависимость константы скорости реакции k от температуры согласно закону Аррениуса выражается формулой:

, (1)

где k0 – предэкспоненциальный множитель; e = 2,718 – основание натуральных логарифмов; Ea – энергия активации, Дж/моль; R=8,315 – универсальная газовая постоянная, Дж/(моль*К); Т – абсолютная температура,К.

Значения k0 и Ea находят, измеряя значения константы скорости k при различных температурах Т. При этом получают набор из n пар значений kiэксп и Тi. Наиболее вероятными значениями k0 и E будут такие, которые при подстановке их величин в формулу (1) дадут значения kiрасч , наиболее близкие к kiэксп .

В общем виде эта задача может быть сформулирована так: имеются две переменные x и y, связанные некоторой зависимостью f, вид которой нам известен. В эту зависимость входят некоторые постоянные a и b, значения которых нам неизвестны. При переходе к логарифмической форме уравнения (1) и заменяя y=ln(k),x=1/T,a=-E/R,b=ln(k0), имеем линейную зависимость:

. (2)

Для того, чтобы найти наиболее вероятные значения a и b, мы провели серию измерений x и y, т.е. нашли n пар значений xiэксп и yiэксп. Требуется найти такие значения a и b, которые при подстановке в зависимость (2) совместно с xiэксп дали бы значения yiрасч, наиболее близкие к yiэксп. За меру близости берут величину:

. (3)

Требуется найти минимум функции s. Это достигается решением системы уравнений

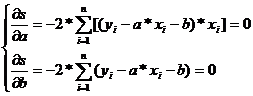(4)

Раскрывая знаки сумм и решая систему относительно неизвестных a и b, получаем формулы для нахождения наиболее вероятных значений a и b:

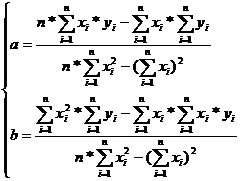(5)

Расчет значений a и b на основе данных таблицы 1 осуществлен с использованием электронных таблиц Excel(см. Приложение 1). Полученные значения: a=-7273,034, b=9,830637.

Применяя формулы k0=exp(b), E=-R*a, получаем экспериментальные значения параметров уравнения Аррениуса:

k0=18594,79, E=60468,01 Дж/(моль*К).

Практически всегда, кроме знания величин a и b, требуется определить и их погрешности Δa и Δb с некоторой степенью достоверности α. Поскольку измерения проводились с некоторой погрешностью, то yiрасч и yiэксп будут отличаться. Этот разброс характеризуется дисперсией s0, где

, (6)

где m=2 – количество определяемых констант.

Согласно Приложению 1 =0,001621.

Определение параметров a и b можно рассматривать как результат косвенных измерений. Для того, чтобы оценить точность определения параметра, можно воспользоваться законом накопления ошибок. Тогда дисперсии параметров a и b:

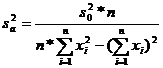, (7а)

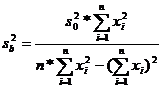. (7б)

=7991,043,=0,013721.

Погрешности определения параметров a и b:

, (8а)

, (8б)

где t – значение критерия Стьюдента для степени достоверности α (α=0,95) и степени свободы f=n-1.

Δa=199,3,Δb=0,26.

Погрешности определяемых k0 и E: Δk0=k0*Δb=4857,21; ΔE=R*Δa=1657,36.