Теплопроводность в зернистом слое в условиях естественной
конвекцииСтатьи / Теплопроводность в сплошных средах и двухфазных, продуваемых и непродуваемых телах (слоях) / Теплопроводность в зернистом слое в условиях естественной
конвекции
При наличии градиента температуры в зернистом слое, заполненном жидкостью или газом достаточно большой плотности, может возникнуть естественная конвекция, приводящая к заметному увеличению эффективного коэффициента теплопроводности.
С возможностью естественной конвекции нужно считаться при процессах горения в шахтных топках и газогенераторах, при каталитических процессах в начальных участках реакторов с большим градиентом темепратуры и концентрации, в доменных печах, в тепловой изоляции в виде зернистой засыпки.
Рассмотрим зернистый слой высотой x, имеющий температуру верхнего торца t2 и нижнего торца t1, причем t1>t2. При отсутствии конвективных потоков газа в слое установится одномерный тепловой поток q, определяемый коэффициентом теплопроводности lоэ при линейном распределении температуры по высоте слоя. Примем далее, что в направлении, одинаковом с направлением теплового потока, движется поток газа (жидкости) с массовой скоростью G; распределение температуры по высоте слоя остается неизменным и одинаковым для обеих фаз. Такое допущение оправдано, если основное количество теплоты передается теплопроводностью. Конвективный тепловой поток:
qк=СpG(t1-t2) (VI)
Конвективная составляющая коэффициента теплопроводности описывается выражением:
lк=qк/(t1-t2)/x=CpGx (VII)
а суммарная теплопроводность слоя при наличии конвекции равна:
lэ=lоэ+lк (VIII)
В рассматриваемом случае естественная конвекция в слое вызвана различием плотности газа за пределами слоя при t2 и средней плотности в слое при температуре 0.5(t1+t2).
Dr=0.5rbtDt (IX)
где bt - коэффициент объемного расширения газа; Dt=t1-t2.
где С=e3/a2K - коэффициент проницаемости слоя, зависящий от его структуры.
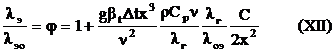 |
Здесь:
![]()
- критерий Грасгофа, отнесенный к разнице температур в слое; в качестве определяющего размера принята высота слоя;
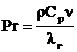
- критерий Прандтля для газовой среды;
![]()
- критерий Релея для зернистого слоя.
В отличие от аналогичного критерия GrPr, применяемого для описания естественной конвекции в однофазной среде, а Ra входят два симплекса, отражающие тепловые и гидравлические свойства зернистого слоя.
С учетом принятых обозначений:
j=1+0.5Ra (XIII)
В более общем случае, когда естественная конвекция возникает в замкнутом с торцов зернистом слое, коэффициент в формуле (XIII) должен измениться. Кроме того, нарушение устойчивости газовой среды в слое и начало естественной конвекции должно определяться некоторым критическим значением Ra0, так же, как это имеет место в однофазной среде.
В соответствии с этим формула (XIII) приобретает вид:
j=1+y(Ra-Ra0) (XIV)
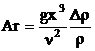 |
Смотрите также
Круговорот веществ в природе
...
Плутоний (Plutonium), Pu
Изотоп плутония 238Pu впервые искусственно получен 23.02.1941 года группой американских ученых во главе с Г. Сиборгом путем облучения ядер урана дейтронами. Примечательно, что только после искусственн ...
