Активационное уравнение Аррениуса

1.1. Вывод уравнения активации по Вант-Гоффу:

Из уравнения изохоры Вант-Гоффа для обратимой реакции, содержащей прямую и обратную стадии , получаем

(5.1)

Для отдельных стадий: 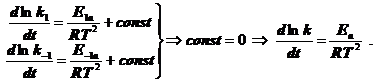(5.2)

1.2.Вывод уравнения активации по Аррениусу:

Реакция рассматривается как состоящая из двух гипотетических стадий. На первой устанавливается равновесие между исходными и активными частицами. На второй протекает собственно превращение активных частиц в продукт.

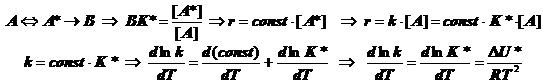(5.3)

Обозначим и получаем активационное уравнение Аррениуса:

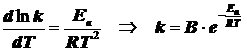. (5.4)

Последнее выражение получается, если принять простейшее допущение и считать энергию активации постоянной и не зависящей от температуры. Это справедливо для небольших интервалов температуры. В большинстве приложений уравнение Аррениуса является основой экспериментального определения активационных параметров химической реакции. Простейший способ – графический. Аррениусовскими координатами называют переменные (1/T; lnk ). В этих переменных экспериментальные данные ложатся на прямолинейный график: Рис.10.

Угловой коэффициент этой линейной функции в нормальных случаях отрицателен и даёт возможность определить энергию активации. Самый смысл энергии активации говорит о том, что эта величина по знаку должна быть положительна. Если всё же наклон прямой в аррениусовских координатах окажется положительным, то это означает отрицательный знак кажущейся энергии активации, и это прямое указание на сложный механизм реакции, и такое усложнение может иметь место уже в самом элементарном акте. Подобная ситуация наблюдается у тримолекулярных реакций .

2) Молекулярные модели химического элементарного акта

2.1. Теория Активных Соударений (ТАС)

2.1.1. Число двойных соударений между одинаковыми частицами

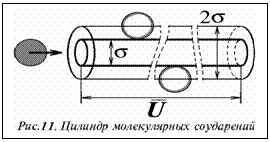
Одна частица в единицу времени пробежит «цилиндр соударения» (рис.), в котором затронет любую частицу, центр которой в него попадает, и его объём выражается через среднюю скорость частицы u и её диаметр :

(5.6)

Число частиц в этом цилиндре пропорционально его объёму и мольной концентрации. С ними-то и сталкивается одна частица. Полное же число столкновений в единичном объёме Z’ должно бы быть равно половине от произведе­ния числа соударений одной частицы на число всех частиц в объёме (удобно выразить его через мольную концентрацию), но, согласно газокинетической теории Максвелла, истинное число соударений Z превышает Z’ в 21/2 раз из-за ломаного характера траектории, увеличивающего вероятность встреч частиц в пространстве. Необходимые формулы имеют вид:

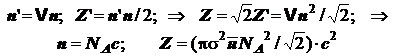(5.7)

Примечание: Неискушённый читатель вправе удивиться столь простому и решительному способу подсчёта числа столкновений частиц – ведь, всякое соударение изменяет вектор скорости, и реальная траектория это ломаная линия. Однако учтём, что при упругом ударе изменяется лишь направление, а не модуль вектора скорости, и поэтому длина ломаной траектории, образуемой за единицу времени, остаётся равной линейной скорости частицы. Это подобно тому, как длина столярной складной линейки суммируется из её отдельных сегментов. Полезно отметить, что и уточнение числа соударений за счёт учёта постоянной смены ориентации движений, носит формальный характер, не меняя существа дела. Добавим, что газокинетический диаметр частиц понятие до известной степени условное и вводится для упрощения модели.

2.1.2. Число соударений между разными частицами (частицы вида 1 и частицы вида 2)

В формулу средней скорости следует подставить усреднённый диаметр и приведённую массу, и также нет необходимости уменьшать число соударений вдвое. Все прочие соображения те же самые . Поэтому при наличии всех сомножителей со слегка изменённым смыслом численный множитель возрастёт вдвое . Действительно, получаем

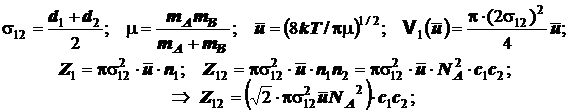(5.8)

2.1.3. Число «горячих» частиц одного вида равно , откуда получаем: