В первом – адиабатическом – приближении, предложенном М. Борном и Р. Оппенгеймером в 1927 году, полагают, что движение электронов можно рассматривать как независимое от медленного движения ядер, так как массы ядер значительно (на 3-4 порядка) превышают массу электронов. Решение задачи в этом случае разбивается на два этапа: сначала решают уравнение Шредингера только для электронной части гамильтониана при фиксированном положении ядер. При этом волновая функция должна быть асимметричной по отношению к перестановке электронов, т.е. при перестановке двух электронов с одинаковыми спинами полная волновая функция должна менять знак (принцип Паули). Затем решают задачу о движении (колебании) ядер в поле потенциала, полученного при решении предыдущей задачи, при этом получают значения колебательной энергии молекулы.

Основы квантовой теории многоэлектронных систем были заложены в работах В.Гейзенберга, В. Гайтлера и Ф. Лондона (1926 – 1927 г.г.). Они показали, что существование, устойчивость и свойства этих систем невозможно объяснить в рамках классических представлений. Согласно Гайтлеру и Лондону, связывание между атомами и молекулами в молекуле водорода обусловлено т.н. обменным взаимодействием.

Дальнейшее развитие теории многоэлектронных атомов связано с методом самосогласованного поля, предложенного в 1927 году Д.Р.Хартли. В нем взаимодействие каждого из электронов со всеми остальными заменяется взаимодействием с усредненным полем, создаваемым остальными электронами. В 1930 году В.А.Фок усовершенствовал метод Хартли, использовав для многоэлектронной волновой функции представление в виде слейтеровского детерминанта:

,

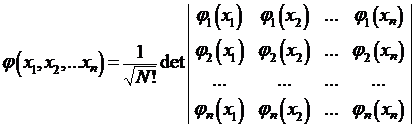где φj(xj) – одноэлектронная спин-орбиталь, xj = (rj, αj), где rj – пространственные координаты, αj – спиновые координаты.

Такой вид волновой функции позволяет учесть принцип Паули. Одноэлектронные функции (орбитали) находят, решая уравнение Хартли-Фока:

Fφi = εiφi,

где F – оператор, называемый фоксианом;

εi – энергии i-той заполненной орбитали.

Система уравнений Хартли-Фока является системой нелинейных интегро-дифференциальных уравнений, которые можно решать методом итераций.