4.3.8.1. Использование операторов сдвигов состояний позволяет также максимально просто найти собственные функций операторов и без каких-либо специальных сведений о дифференциаль­ных уравнениях. Авторы сознательно построили настоящий раздел в расчёте на внимательного читателя-химика, владеющего лишь мини­мальными, но достаточно прочными навыками в области тригонометрии и математического анализа.

4.3.8.2. Прежде всего, выпишем операторы повышения и понижения в сферических координатах, используя формулы (4.53) и (4.54):

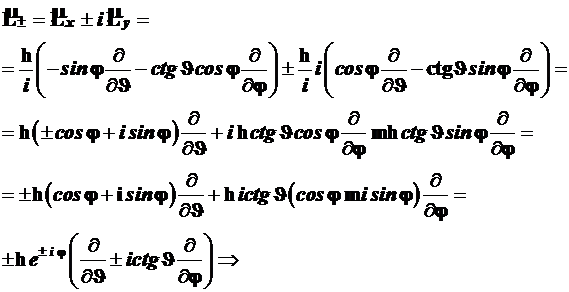
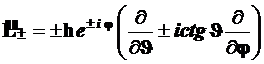(4.109)

В силу того, что собственные функции, получающиеся в результате действия операторов сдвига, подлежат нормировке, как это уже об­суждалось в разделе 4.3.5.10., мы имеем все основания определить эти операторы с точностью до постоянного множителя, т.е. вместо (4.109) ограничимся выражением

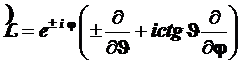(4.110)

4.3.8.3. Исходные уравнения для вывода всей цепочки волновых функций – уравнения аннигиляции

(4.111)

На основании формул (4.50) и (3.28) функцию мож­но представить в виде

(4.112)

С учётом этого уравнение (4.111) в сферических координатах: запишется в форме

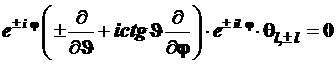. (4.113)

Совершим очень несложные преобразования, приводя к дифференциальному уравнению для функции:

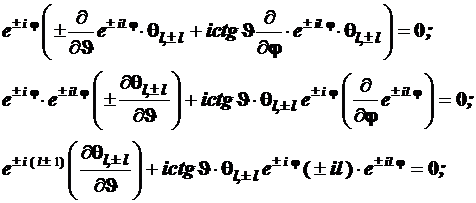
откуда следует 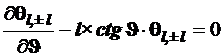(4.114)

4.3.8.4. Разделяя переменные, получаем

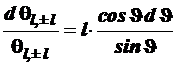(4.115)

Учтём что ,

(4.116)

Интегрирование уравнения (4.116) даёт

(4.117)

где – постоянная интегрирования, определяемая из условия нормировки. Окончательно получаем формулу для функции

(4.118)

4.3.8.5.Формула (4.118) дает лишь предельные выражения волно­вых функций , отвечающие максимальному и минимальному значе­ниям квантового числа m, а именно и , или что то же самое . Все волновые функции, соответствующие промежуточным значениям очень просто получаются последовательным действием операторов с точностью до нормировочных множителей, которые могут быть рассчитаны в каждом конкретном случае

4.3.8.6.Отметим, что мы не ставим перед собой и перед читате­лем задачу вывода общей формулы сферических волновых функций. Это связано, с одной стороны, с тем, что она обязательно покажется сли­шком перегруженной индексами и коэффициентами, к которым удобнее привыкать постепенно. С другой стороны, для практических целей ред­ко требуются функции с большими значениями квантового числа l. В химическом обиходе встречается состояния с l = 0, 1, 2, 3, по­этому ограничимся этими значениями, (их символы см. в табл. 4.5 ).

4.3.8.7. Итак, нас будут интересовать s–, p–, d–, f– орбитали жесткого ротатора. Запишем соответствующие исходные функции и , с точностью до постоянного множителя:

для s-состояния и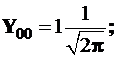

для p- состояния и

для d- состояния и

для f- состояния и

4.3.8.8. Орбиталь s –типа – лишь одна и волновая пункция тре­бует только нормировки. Поскольку сомножитель 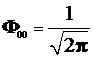уже нормирован, достаточно пронормировать функцию . Выделяя из эле­мента конфигурационного пространства (см. рис 4.3) все со­множители, определенные на переменной , получаем