Для решения задач связанных с нахождением температурного поля необходимо иметь дифференциальное уравнение теплопроводности. Под дифференциальным уравнением понимают математическую зависимость между физи­ческими величинами характеризую­щими изучаемое явление, причем эти физические величины являются функциями пространства и времени. Такое уравнение характеризует протекание физического явления в любой точке тела в любой момент времени.

Дифференциальное уравнение теплопроводности дает зависимость между температурой, временем и координатами элементарного объе­ма.

Вывод дифференциального урав­нения сделаем упрощенным мето­дом. Предположим, что имеется од­номерное температурное поле (теп­ло распространяется в одном нап­равлении, например в направлении оси х ). Термические коэффициенты считаем не зависимыми от координат и времени.

Выделим в однородной и изотропной неограниченной пластине эле­ментарный параллелепипед, объем которого равен (рис. 3.1) Количество тепла, втекающего через левую грань в параллелепи­пед в единицу времени, равно а количество тепла, вытекающе­го через противоположную грань в единицу

времени, равно

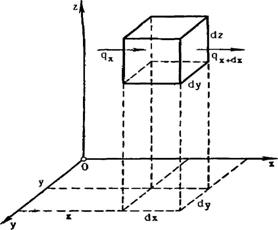
Рис 1.3. Поток тепла через элементарный объём

Если , то элементарный параллелепипед будет нагреваться, тогда разница между этими потоками тепла по закону сохранения энергии равна теплу, аккумулированному данным элементарным парал­лелепипедом, т. е.

(3.1)

Величина есть неизвестная функция х. Если ее разложить в ряд Тейлора и ограничиться двумя первыми членами ряда, то можно написать:

(3.2)

Тогда из равенства (3.1) будем иметь:

(3.3)

Применяя уравнение теплопроводности , получим:

(3.4)

Уравнение (3.5) есть дифференциальное уравнение теплопроводности для одномерного потока тепла. Если тепло распространяется по нормали к изотермическим поверхностям, то вектор q можно разложить на три составляющие по координатным осям. Количество аккумулированного элементарным объемом тепла будет равно сумме

(3.5)

Тогда дифференциальное уравнение примет вид

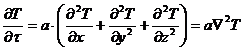(3.6)

Для симметричного одномерного температурного поля является функцией одной координаты. Поясним это на примере бесконечного круглого цилиндра. Если ось такого цилиндра совпадает с координа­той z, то температура в любой точке цилиндра будет зависеть только от координат х и у. При равномерном охлаждении или нагревании ци­линдра в любой точке, отстоящей на расстоянии r от оси цилиндра, температура в данный момент времени будет одна и та же. Следова­тельно, изотермические поверхности будут представлять собой цилин­дрические поверхности, коаксиально расположенные к поверхности ци­линдра. Между радиальной координатой r (радиус-вектор) и координатами х и у существует связь

r2 = х2 + у2.

(3.7)

Тогда дифференциальное уравнение теплопроводности для бесконечного цилиндра можно преобразовать так:

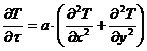(3.8)

для бесконечного цилиндра можно преобразовать так:

(3.9)

(3.10)

Дифференцируя (3.8) по х, а (3.10) по у, получаем

(3.11)

(3.12)

Складывая уравнения (3.11) и (3.12) и принимая во внимание (3.7), получим для уравнения теплопроводности следующее выражение:

В общем случае, когда температура зависит от всех трех координат (х, у, г), дифференциальное уравнение теплопроводности конечного ци­линдра имеет вид

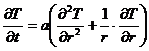; (3.13)