Рас­смотрим неограниченный цилиндр радиуса R, температура поверх­ности которого остается неизмен­ной на протяжении всего процес­са теплообмена. Радиальное рас­пределение температур в началь­ный момент задано в виде некоторой функции Т(r). Необходимо найти распределение температур определения в цилиндре в любой момент времени. Задачи такого типа встречаются при расчете процессов охлаждения полимерного волокна, затвердевания литников литьевых форм и т. п.

Дифференциальное уравнение теплопроводности для цилиндра

имеет вид: 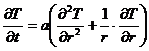(2.19)

Краевые условия:

Решение, полученное методом разделения переменных, в без­размерной форме, имеет вид:

(2.20)

Для оценки изменения теплосодержания цилиндра определим среднюю температуру как:

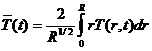(2.21)

Тогда безразмерная средняя температура определится соотноше­нием: (2.22)

где ; - корни функции Бесселя первого рода нулевого порядка определяемые выражением:

(2.23)

Таким образом, уменьшение средней температуры описывается простым экспоненциальным законом. Для удобства прикидочных расчетов на рис. IV. 10 приведена номограмма зависимости между q и Fo.

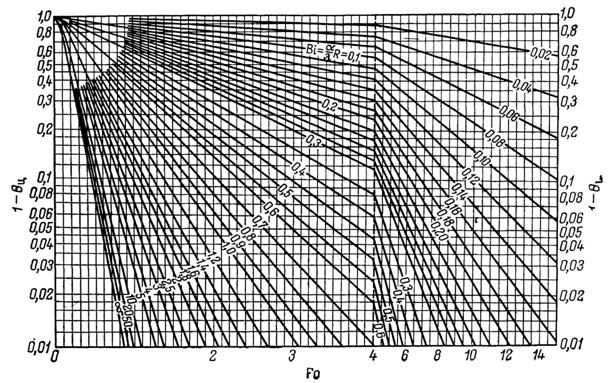
Рис. 2.5 Номограмма для определения зависимости между безразмерной средней избы­точной температурой и критерием Фурье в случае неограниченного цилиндра.