Растворы, содержащие заряженные частицы обладают особыми физико-химическими свойствами, что обусловлено дальнодействующим электростатическим потенциалом, спадающим с расстоянием г по закону г ~1. Уже при небольших концентрациях электролита отчетливо проявляется неидеальность раствора. Добавки индифферентной соли сильно влияют на стабильность дисперсных систем, а также на скорости реакций и на кривые титрования. Различные электролиты существенно влияют на состояние ПАВ и полимеров в растворах. Например, введение индифферентного электролита в растворы ионных ПАВ заметно понижает величину KKM.

Таким образом, электростатические эффекты разнообразны и характерны для растворов. К счастью, качественно, а иногда и количественно в них можно разобраться на основе простой теории Дебая-Хюккеля.

Электростатический потенциал связан с распределением заряда уравнением Пуассона-Больцмана:

где Д - оператор Лапласа:

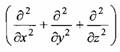
Задача сильно упрощается для сферически симметричных систем, поскольку в этом случае оператор Лапласа выражается соотношением

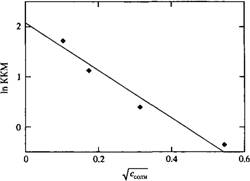
Влияние концентрации соли на ККМ. Прямая линия проведена с максимальным приближением к экспериментальным данным. Теория Дебая-Хюккеля предсказывает линейность между KKM и Соли.

Теперь нужно найти выражение для распределения заряда, отражающее "самораспределение" ионов под действием электростатического потенциала.

Принимая, что распределение ионов вокруг центрального иона, расположенного в начале координат, подчиняется распределению Больцмана:

приходим к уравнению Пуассона-Больцмана:

где Z - зарядовое число иона, кв - константа Больцмана, T - температура и coi - концентрации ионов на бесконечном удалении. Это нелинейное уравнение, и его решение обычно сопряжено с большими трудностями. Если для преобразования уравнения воспользоваться разложением экспоненты в ряд, получим более простое уравнение

в котором вводится новый параметр - дебаевский радиус экранирования к-1. Конечное выражение для электростатического потенциала имеет вид:

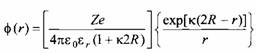
где R - радиус иона. Уравнение имеет уже достаточно простой вид и является очень важным. Из него вытекает, что потенциал вокруг иона в растворе соли не спадает с расстоянием по закону г _1, а уменьшается как ехр /г. Это означает, что электростатическое взаимодействие имеет гораздо более короткий радиус действия, зависящий от к-1. В свою очередь параметр к-1 зависит от концентрации соли и от зарядов ионов.

Физический смысл этого вывода заключается в том, что центральный ион притягивает противоположно заряженные ионы и отталкивает ионы одного с ним заряда, создавая таким образом экранирование. Другое важное и тоже простое уравнение получено для избыточного химического потенциала, который, согласно теории Дебая-Хюккеля, имеет следующий вид:

Дебаевский радиус экранирования - очень важная величина, использующаяся для качественных и количественных оценок. Из уравнения следует, что вклад электростатических взаимодействий снижается на расстояниях Для водного 1 M раствора 1: 1-валентной соли при комнатной температуре толщина ионной атмосферы равна 3.0 А. Так как к-1 обратно пропорциональна то при концентрации соли 10 мМ к-1 увеличивается до 30 А. Заряд иона также имеет значение. Многозарядные ионы очень эффективно экранируют электростатические взаимодействия. Теория Дебая-Хюккеля прекрасно выполняется для водных растворов 1: 1-валентных солей, но приводит к заниженным оценкам экранирования заряженных агрегатов в присутствии многозарядных противоионов.