Каждая молекула может быть отнесена к одной из точечных групп 14 типов. Эти точечные группы состоят из строго определенных операций симметрии и никакие другие точечные группы невозможны. Однако, сопоставляя молекулу с одной из перечисленных выше групп симметрии, следует тщательно выбирать более полную группу, к которой принадлежит молекула. Неполная группа допускает асимметрию в потенциальном поле вокруг атома, что из физических соображений часто не бывает. Например, плоская молекула ZX3 вряд ли обладает симметрией C3, ибо тогда распределение потенциала могло бы быть такое как на рисунке, хотя совершенно ясно, что оно невозможно физически. Ее симметрия и не D3 (C3, 3C2), ибо в этом случае распределение потенциала могло бы быть пространственно в виде трехлопастного винта. Полная симметрия плоской молекулы типа ZX3 - D3h (C3, 3C2, 3sv, sh).

После установления полной симметрии молекулы можно классифицировать атомы на эквивалентные. Эквивалентными атомами называются атомы, которые переходят друг в друга при всех преобразованиях симметрии. Все эквивалентные атомы, разумеется, одинаковы в химическом отношении. Обратное, конечно, не справедливо. Число эквивалентных атомов не может превышать полный порядок группы (т.е. число операций), однако, может быть меньше. Для любого вида эквивалентных атомов совокупность операций, оставляющих данный атом неизменным, образует подгруппу данной группы G. В частном случае такая подгруппа может либо совпадать с подгруппой G, либо состоять лишь из одного элемента E (C1). Подгруппа атомов X в молекуле ZX3 есть C2v (Е, C2, sv, sh).

Поскольку мы идентифицировали элементы группы симметрии с некоторыми определенными геометрическими операциями, мы постараемся найти для них аналитические выражения, т.е. представления. Сначала мы обсудим геометрический смысл представлений и укажем до какой степени геометрическая интуиция может служить для их нахождения. Вместо действительного указания операций группы мы можем, очевидно, указать численное значение некоторой величины, связанной с симметричной фигурой для каждой из операций. Например, в циклической группе Cn мы можем, начиная с произвольно выбранной точки, обозначить каждую операцию Cnp величиной соответствующего угла вращения

E	Cn1	Cn2	Cn3	Cnk	Cnn
0	1*2p/n	2*2p/n	3*2p/n	k*2p/n	n*2p/n

Недостатком такого "представления" является то, что соответствующая операция с углами не является умножением, а представляет собой сложение с последующим взятием остатка от целого кратного 2p.

Например, 2*2p/5+4*2p/5=12p/5 = 2p+2p/5.

Но одним из требований для пригодных представлений является то, чтобы они имели, как и их операции или обычное, либо матричное умножение. Так в примере с Cn можно вместо значения угла выбрать комплексную координату на единичном круге.

Е	Cn2	Cn3	Cnk	…….	Cnn
ехp (2pi /n)	ехp (2pi /n) 2	ехp (2pi /n) 3	ехp (2pi /n) k	….	ехp (2pi /n) n

Тогда для последовательных преобразований мы будем иметь причем это число будет уже удовлетворительным представителем группы. В более общем случае можно было бы рассматривать три координаты X,Y,Z точки на единичной сфере, и смотреть, что с ними происходит при различных преобразованиях группы. Если операция R группы переводит точку М (X,Y,Z) в положение M¢ (X¢,Y¢,Z¢), то это преобразование координат может быть записано:

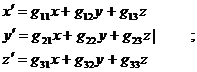
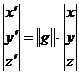
Тогда набору из 9 чисел g11, g12,..., g33 могут быть сопоставлены операции G в качестве ее представления. Однако, единственный путь ввести для этих чисел простые правила умножения - это взять их в виде матрицы:

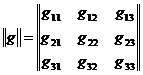
Так, в частности, операция отражения в плоскости sz, операция идентичности Е и инверсии I в начале координат будут иметь вид:

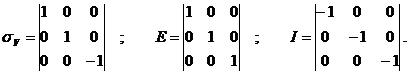
Последовательное применение нескольких операций будет описываться матричным произведением исходных представлений. Действительно, пусть преобразование А дает X¢=АX. Последующее преобразование B дает: X¢¢=BX¢, или через X: X¢¢=BAX, X¢¢=CX, где C=BA.  Преобразование с коэффициентами C является произведением двух преобразований и осуществляет таким образом представление операции C=AB.

В частности, зеркально-поворотная ось четвертого порядка S41=C41*Cn2 может быть представлена матрицей:

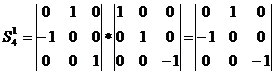
Этот же результат можно было получить, рассматривая непосредственное изменение координат при операции sh и последующей операции C41.

Таблица 2

Таблица умножения группы C4v.

E	C41	C43	C42	sx	sy	sd1	sd2
C43	E	C42	C41	sd1	sd2	sy	sx
C41	C42	E	C43	sd2	sd1	sx	sy
C42	C43	C41	E	sy	sx	sd2	sd1
sx	sd1	sd2	sy	E	C42	C41	C43
sy	sd2	sd1	sx	C42	E	C43	C41
sd1	sy	sx	sd2	C43	C41	E	C42
sd2	sx	sy	sd1	C41	C43	C42	E

Таким образом, каждому преобразованию симметрии можно сопоставить некоторую матрицу. Существует взаимно однозначное соответствие между операциями симметрии и матрицей преобразований пространства. Например, для группы C4v мы можем построить матрицы размером 8х8 следующим образом: представление операции R получается заменой на единицу тех элементов в таблице умножения, которые соответствуют этому элементу; в остальных местах таблицы элементы следует заменить нулями. Таким образом могут быть получены так называемые регулярные представления группы. С помощью матричного умножения можно убедиться, что правила перемножения этих матриц удовлетворяют приведенной таблице умножения, и, таким образом, сами преобразования симметрии и матрицы регулярного представления образуют изоморфные группы.

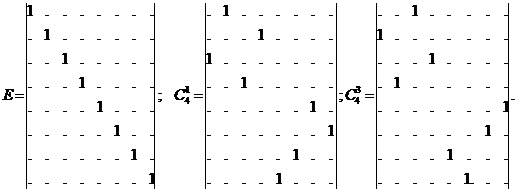
Можно построить для каждого преобразования группы матрицы размерностью 3х3, определяющие преобразование точки трехмерного пространства. Для группы C4v каждому преобразованию симметрии можно сопоставить следующие матрицы преобразования пространства:

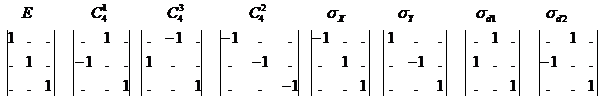
Здесь приведены матрицы преобразования точки на единичной сфере. Они удовлетворяют таблице умножения группы, что легко проверить. Однако, возникает вопрос о том, возможны ли другие способы нахождения представлений. Рассмотрим, например, единичную матрицу (1) и примем E= (1); C41= (1); C42= (1); C43= (1) и так далее. Оказывается, что этот набор матриц тоже удовлетворяет таблице умножения группы, т.е. первоначальный выбор был не самым простым. Поиск других комбинаций матриц первого ранга показывает, что имеется всего четыре таких набора. Пятый набор включает матрицы второго ранга (состоящий из двух столбцов и двух строк), так что это так называемое двумерное представление.

Таблица 3

Представления группы C4v

Пред-ставле-ние	E	C41	C42	C43	sx	sy	sd1	sd2
Г (1)	+ (1)	+ (1)	+ (1)	+ (1)	+ (1)	+ (1)	+ (1)	+ (1)
Г (2)	+ (1)	+ (1)	+ (1)	- (1)	- (1)	- (1)	- (1)	- (1)
Г (3)	+ (1)	- (1)	+ (1)	+ (1)	- (1)	- (1)	- (1)	- (1)
Г (4)	+ (1)	(1)	+ (1)	- (1)	+ (1)	- (1)	- (1)	- (1)
Г (5)	1 0 0 1 1 0 0 1	0-1 1 0 0 1 1 0	-1 0 0-1 1 0 0-1	-1 0 0 1 1 0 0-1	0 1 1 0 0-1 1 0	0 1 1 0 0 0 0 0	1 0 0 1 1 1 1 1	1 0 0 1 0 1 1 0

Пример набора матриц 3*3 уже был рассмотрен. Однако при более детальном рассмотрении обнаруживается, что в действительности матрицы разбиваются на блоки 2*2 и 1*1. Видно, что матрицы, полученные при разбиении на блоки, являются представлениями групп.

Возникают случаи, когда получают матрицы ранга 4*4 или выше, но исследование всех этих матриц показывает, что их всегда можно разбить на блоки более простых матриц, которые для группы C4v всегда связаны с пятью представлениями. Эти пять наборов матриц, таким образом, имеют особое значение, и их называют неприводимыми представлениями. Необходимо заметить, что такой интуитивный метод нахождения представлений делает ясным их геометрический смысл, но имеет серьезные недостатки. Имеется слишком большой произвол в выборе численной величины, ассоциированной с симметричной фигурой и нет простого пути убедиться, все ли возможные представления найдены. Так же мы не знаем, являются ли полученные представления независимыми или нет. Еще одно возражение состоит в том, что никакой наглядный смысл не может быть приписан представлениям с матрицами порядка выше третьего. В результате мы должны употреблять другие, более формальные методы получения представлений за исключением лишь самых простых случаев.

• Симметрия потенциальной и кинетической энергий
• Представления в пространстве 3n координат смещения молекулы
• Свойства характера
• Определение характеров приводимого представления c (r)
• Обозначение типов симметрии (неприводимых представлений)