Математическая модель, прогнозирующая поведение ансамбля растущих или схлопывающихся паровых пузырьков, базируется на модели динамики одиночного пузырька. Принципы построения системы обыкновенных дифференциальных уравнений, описывающих динамику сферического парового пузырька в неограниченном объеме несжимаемой вязкой жидкости с учетом основных определяющих факторов, подробно изложены в работе (2). Эти уравнения дают возможность рассчитать радиус пузырька r(t), давление и радиальную скорость жидкости на границе с пузырьком, соответственно, pr(t) = Pl(R, t) и wR(t) = wi(r, t), а также распределение скорости wl(r, t) и давления Pl(r, t) в окрестности пузырька. Кроме того, рассчитывается изменение температуры Tv(t), плотности rv(t) и давления пара pv(t) внутри пузырька. Предполагается, что эти параметры распределены в пузырьке однородно. Поток теплоты q(t) и массы j(t) через стенку пузырька в процессе испарения и конденсации пара описывается в приближении молекулярно -кинетической теории с учетом скачка температуры на межфазной границе DT = Ts — Tv, так что в общем случае температура жидкости на границе с пузырьком Ts отлична от температуры пара в пузырьке Tv . Распределение температуры в жидкости в окрестности пузырька Tl (r, t) в процессе его роста или сжатия рассматривается в терминах интегрального метода, в рамках которого получено дифференциальное уравнение изменения толщины теплового пограничного слоя в жидкой фазе. В работе (2) приведены также полуэмпирические уравнения, которые с достаточно высокой точностью аппроксимируют температурные зависимости таких теплофизических параметров воды и водяного пара, как скрытая теплота испарения, поверхностное натяжение, плотность насыщенного пара, плотность и вязкость жидкости для всего температурного интервала существования жидкой фазы вплоть до Тсr. Достоверность модели подтверждается удовлетворительным согласием полученных с ее помощью расчетных результатов с известными в литературе экспериментальными данными по росту и схлопыванию одиночных паровых пузырьков в воде в широком интервале изменения режимных параметров.

Уравнения динамики одиночного пузырька положены в основу модели эволюции неограниченного монодисперсного ансамбля паровых пузырьков, которая учитывает динамическое взаимодействие пузырьков и их коллективное влияние на характер микротечений в межпузырьковом пространстве. Кроме основных уравнений динамики одиночного пузырька система уравнений, описывающих поведение ансамбля, включает дифференциальное уравнение для расчета средней температуры жидкости, которая не остается постоянной благодаря интенсивному испарению при формировании паровой фазы. Модель динамики пузырьков в ансамбле подробно рассматривается в работе (3). Предполагается, что динамическое развитие пузырьков в ансамбле обусловлено нарушением термодинамического равновесия вследствие быстрого изменения внешнего давления.

Поведение пузырьков в ансамбле рассматривается в приближении ячеечной модели, основные положения которой изложены, например, в работе [4]. Весь объем жидкости в монодисперсном пузырьковом ансамбле разбивается на идентичные сферические ячейки, в центре которых находятся сферические пузырьки. Радиус ячейки x связан с величиной текущего паросодержания b соотношением x= R • b-0.33 .Распределение давления зависит от текущих значений размера пузырьков и скорости их роста, а также от количества пузырьков в единице массы Nb, которое в отсутствие коагуляции или дробления пузырьков остается неизменным.

При заданной концентрации Nb величина объемного паросодержания определяется выражением

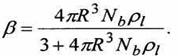(1)

Для анализа поведения ансамбля в целом достаточно рассмотреть ситуацию в отдельной ячейке. При росте пузырька в его окрестности в пределах R ≤ r ≤x появляется сферически-симметричное распределение давления

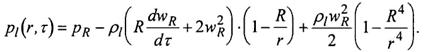(2)

Подстановка в (2) значения дает возможность найти давление в жидкости на внешней границе ячейки.