Аудиторное упражнение. Аллил в методе МОХ
Статьи / Теория МОХ / Аудиторное упражнение. Аллил в методе МОХ

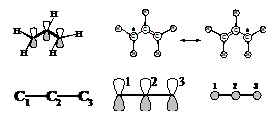
Удобен в качестве простейшего примера -радикал аллил H2C=CH-CH2·.

ВНИМАНИЕ!

А.

В МОХ диагональный элемент векового детерминанта упрощается делением всех элементов на параметр с дальнейшей подстановкой ® (-E)/ =X;

Б. В процессе решения векового уравнения и вычисления индексов электронной структуры МО нумеруются в порядке возрастания энергии. Энергия первого уровня минимальна.

Подпись: В. Истинный знакк хюккелевских интегральных эффективных величин – параметров  отрицательный.

Вековое уравнение и его решение :

(a-E

) b 0

b (a-E

) b = 0;

0 b (a-E

)  

X 1 0

1 X 1 = 0; ® X3-2X=0; X3,2,1=-21/2; 0; +21/2; ®

0 1 X ® E1,2,3=+21/2×; ; -21/2×.

Нормировка МО аллила в МОХ: ci12 + ci2 2 + ci3 2 =1.

Для хюккелевских МО вычисляется нормировочный множитель МО.

.из ненормированных коэффициентов (Ai1, Ai2, Ai3): Ni=(Ai12+Ai22+Ai32)-1/2.

Смотрите также

Свидетельство Никола Фламеля
(Существует несколько версий истории Никола Фламеля, рассказанной им самим. Они изложены у Уэйта в «Алхимиках сквозь века», у Кокрена в «Алхимии — заново открытой и восстановленной в правах» и у С ...

Методы обессоливания нефти и нефтяного сырья (тяжелых остатков)
          Степень подготовки нефти, поставляемой на нефтеперерабатывающие заводы, определена ГОСТ 9965-76.           В зависимости от содержания в нефти хлоридов и воды установлены три г ...

Заключение
1) Методами рН-метрического титрования и вискозиметрии обнаружили и доказали комплексообразование в системе поливинилпирролидон-Са2+. 2) Изучили влияние температуры на стабильность образовавшего ...