Матрица (X—Х)'(Х—) —квадратная, симметричная и положи­тельно определенная. Такие матрицы проявляют некоторые свой­ства, особенно полезные при анализе данных:

· собственные значения, действительные, а также положитель­ные или равные нулю;

· число ненулевых собственных значений равняется рангу мат­рицы;

· два собственных вектора, связанные с двумя различными соб­ственными значениями ортогональны.

В качестве иллюстрации этих свойств, а также чтобы пока­зать их важность при анализе данных можно взять матрицу дисперсий-ковариаций и определим собственные значения матрицы методом наименьших квадратов.

Решая уравнение, получаем два собственных значения:

= 0 ,

что дает =1 и =0,6.

Как , так и действительны и положительны. Ранг матрицы должен равняться 2, поскольку в системе существуют два ненуле­вых собственных значения. Компоненты собственных векторов, связанные с каждым из собственных значений, получаем из опре­деления собственных векторов следующим образом:

для первого собственного значения

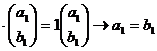
для второго собственного значения

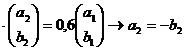
Отметим, что два связанных с каждым из собственных зна­чений вектора действительно ортогональны (т. е. их скалярное произведение равно нулю). В этих двух наборах векторов мы можем выбрать два нормированных вектора, которые соответствен­но составляют ортогональный базис:

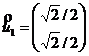
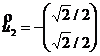
Векторы и действительно аналогичны тем, которые опре­делены в разделе 5.2.1, а координаты матрицы данных относитель­но этой точки отклика уже вычислены:

(Y) = (X-) (U)