В этом пункте данного реферата будет описано одно практически полезное ортогональ­ное разложение т x n - матрицы А. Мы покажем здесь, что невырожденную под­матрицу R матрицы A можно еще более упростить так, чтобы она стала невырожден­ной диагональной матрицей. Получаемое в результате разложение особенно полезно при анализе влияния ошибок входной информации на решение задачи НК.

Это разложение тесно связано со спектральным разложением симметрич­ных неотрицательно определенных матриц ATA и AAT.

Теорема

(сингулярное разложение). Пусть А - m x n -матрица ранга k. Тогда существуют ортогональная m x m матрица U, ортогональ­ная n x n -матрица V и диагональная m x n -матрица S) такие, что

Матрицу S можно выбрать так, чтобы ее диагональные элементы составля­ли невозрастающую последовательность; все эти элементы неотрицательны и ровно k из них строго положительны.

Диагональные элементы S называются сингулярными числами А.

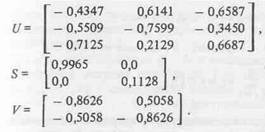
Доказательства данной теоремы приводить не имеет смысла во избежание нагромождения множества сложных математических выкладок, прямого отношения к теме, рассматриваемой в данном реферате, не имеющих. Ограничимся следующим численным примером, в котором дано сингулярное разложение матри­цы А вида: