2.5.1. Среднее значение динамической переменной , получаемое из множества измерений, равно математическому ожиданию этой величины:

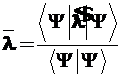(2.30)

Если волновая функция нормирована, то знаменатель единичен, и получаем более простое выражение;

(2.31)

2.5.2. Покажем, что у чистых состояний квантово-механической системы средние значения наблюдаемых переменных совпадают с собственными значениями соответствующих эрмитовых операторов. В этом случае формулы (2.30) и (2.31) непосредственно следуют из фундаментального операторного уравнения (1.1).

Чтобы показать это, запишем уравнение (1.1) с помощью символики Дирака, далее слева скалярно домножим каждую его часть на бра-вектор | и выделим в правой части равенства собственное число . В итоге приходим к формулам (2.30) и (2.31). Цепочка простейших преобразований имеет вид:

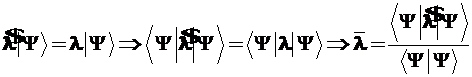
Для общего случая смешанных состояний подобного обоснования нет, и формулы (2.30) и (2.31) постулируются. Этот постулат приобретает уже универсальное содержание. С его помощью можно рассчитывать средние значения даже тех динамических переменных, операторы которых не обладают дискретными спектрами волновых функций и собственных значений, например, координаты и потенциальной энергии.