В прошедшее десятилетие было предпринято очень много попыток описать математически процессы, протекающие при восстановлении оксида азота. В частности, при помощи математических моделей изучались эффекты массопереноса на блочном катализаторе. Была разработана двухмерная математическую модель для движения газового потока в слое катализатора, в которой особое внимание уделялось таким параметрам, как скорость движения потока, а, следовательно, и режим течения газового потока, диаметр монолитного канала, коэффициент диффузии и скорость химической реакции. Адекватность предложенной модели была проверена путем сравнения расчетных данных с экспериментальными. Сравнение показало, что и внутре-, и внешнедиффузионные ограничения должны приниматься во внимание, особенно при высоких температурах.

Работы этих ученых показали, что математическое моделирование процессов является очень перспективным и достаточно точным методом изучения химических процессов вообще и процессов восстановления оксидов азота в частности.

Математическая модель определяется лимитирующей стадией процесса. В случае, когда лимитирующей стадией является химическая реакция, математическая модель будет включать в себя дифференциальные уравнения первого порядка, описывающие изменение концентрации каждого вещества во времени:

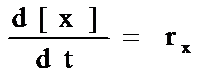
где [x] – концентрация интересующего нас вещества,

t – время,

rx – скорость изменения концентрации данного вещества во времени, имеющая, следующий вид:

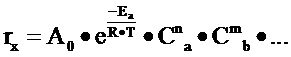
, где

- предэкспоненциальный множитель,

энергия активации процесса,

R – универсальная газовая постоянная,

С – концентрации реагентов

m, n – порядок реакции по веществам a и b соответственно. В данной работе все порядки приняты равными единице.

Если же лимитирующей стадией процесса является внутренняя или внешняя диффузия, математическая модель будет состоять из дифференциальных уравнений второго порядка. В эти уравнения входят также такие параметры, как скорость движения потока, размер пор катализатора, коэффициент диффузии. Такие зависимости позволяют определить концентрацию вещества в зависимости от длины реактора и расстояния от его оси. Вид этих уравнений представлен ниже.

Для нахождения концентрации вещества в потоке:

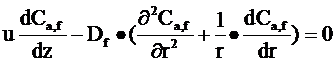
Для нахождения концентрации вещества на поверхности и внутри катализатора:

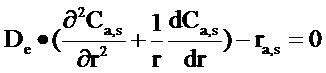
Скорость реакции разложения оксида азота описывается при помощи кинетической модели по механизму Лэнгмюра-Хиншельвуда:

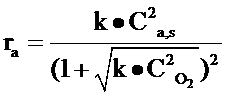
Перечень символов:

- концентрация в потоке;

- концентрация в твердой фазе (на поверхности катализатора и внутри его пор;

- коэффициент эффективной диффузии;

r – радиальная координата;

- коэффициент молекулярной диффузии;