Дисперсные системыМатериалы / Дисперсные системыСтраница 9
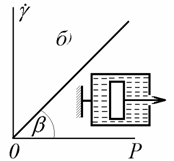
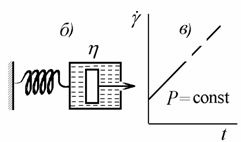
Вязкое течение описывают уравнением Ньютона (2.4.1, а) в форме ![]() . Схема модели вязкого течения и зависимость градиента скорости смещения от напряжения приведены на рис. 2.31, б. Вязкость жидкости определяется как сtgb. В качестве механической модели идеальной вязкой ньютоновской жидкости служит поршень в цилиндре, между которыми возможно перетекание.
. Схема модели вязкого течения и зависимость градиента скорости смещения от напряжения приведены на рис. 2.31, б. Вязкость жидкости определяется как сtgb. В качестве механической модели идеальной вязкой ньютоновской жидкости служит поршень в цилиндре, между которыми возможно перетекание.
|
|
|
|
|
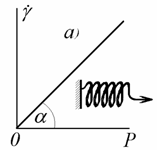
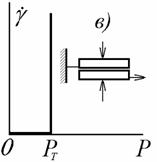
Рис. 2.31. Модель и зависимость деформации от напряжения: а – идеально упругого тела (Гука); б – идеально вязкой жидкости (Ньютона); в – идеально пластического тела (Кулона) |
Физическая модель вязкого течения связана с термически активируемым процессом перестройки взаимодействующих друг с
другом молекул. Естественно, что при действии напряжения одни связи между молекулами жидкости разрываются, а другие – образуются вновь. В истинно вязкой ньютоновской жидкости коэффициент вязкости остается постоянным от очень малых нагрузок вплоть до напряжений, при которых ламинарный режим течения переходит в турбулентный. В ряде случаев при изучении вязкого течения используют величину, обратную вязкости, которую называют текучестью.
Пластичность, или пластическое течение, не является линейной функцией напряжения. В качестве модели пластической деформации используют твердое тело, лежащее на плоскости (рис. 2.31, в) и удерживаемое на месте силами сухого трения вплоть до некоторого напряжения, способного преодолеть это сухое (кулоновское) трение. Такое течение возможно, например, в пастах пигментов, когда происходит последовательное разрушение-восстановление контактов между частицами, которые фиксируются в пространстве через некоторую прослойку жидкой фазы. В том случае, если в системе образуется кристаллическая структура при непосредственном контакте между частицами, течение начнется только после необратимого разрушения таких контактов и критическое напряжение будет соответствовать их прочности.
|
|
|
|
Рис. 2.32. Зависимость напряжения (а) и деформации (в) от времени и модель Максвелла (б) | |
Конечно, в практическом приложении структурообразования
и разрушения (например, при разрушении структуры в загущенных полимерами печатных красках при перемешивании и в процессе ее нанесения на ткань и при восстановлении структуры в том рисунке, который нанесен на ткань, или при нанесении раствора полимера - шлихтующего препарата - на нити), одновременно могут проявляться и различные виды деформаций: упругая деформация, затем вязкое или пластическое течение и последующее структурирование.
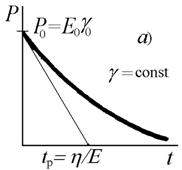
Если в системе внешнее напряжение расходуется на преодоление упругой деформации и вязкого течения, то используют модель, предложенную Максвеллом, из последовательно соединенных элементов моделей Гука и Ньютона (рис. 2.32, а). В таких системах типично проявление релаксации напряжения, описываемого уравнением
P0(t) = P0exp( t/tp), (2.4.55)
где P0= E0g0 – начальное напряжение; tр= h/Е – время релаксации.
При t < tp система ведет себя как твердое тело. При t>>tp модель Максвелла соответствует жидкоподобному течению. Явление релаксации связано с тем, что для перестройки структуры при относительно невысоком напряжении требуется определенное время. Поэтому при кратковременном (мгновенном) приложении напряжения в системе возникают постепенно снижающиеся внутренние напряжения. Возможно, что снятие внутреннего напряжения будет реализовано при t®¥. Для жидкости, описываемой моделью Максвелла, характерна необратимость деформации.
Смотрите также
Задание 3
Закончите уравнения химических реакций:
H2O2+K2Cr2O7+H2SO4→
KHSO4+KMnO4+H2O→
2.Определите формулу вещества, если известно, что оно содержит 7.69% Ag, 23.08% N, 46.15%H,
23.08% O ...
Моделирование процессов переработки пластмасс
Курсовая работа
содержит расчет температурного поля литникового канала литьевой формы, теоретические
сведения о процессах происходящих в химической технологии связанных с
охлаждением и наг ...